CAÍDA LIBRE
En física, se denomina caída libre al movimiento de un cuerpo bajo la acción exclusiva de un campo gravitatorio. Esta definición formal excluye a todas las caídas reales influenciadas en mayor o menor medida por la resistencia aerodinámica del aire, así como a cualquier otra que tenga lugar en el seno de un fluido; sin embargo, es frecuente también referirse coloquialmente a éstas como caídas libres, aunque los efectos de la viscosidad del medio no sean por lo general despreciables.
El concepto es aplicable también a objetos en movimiento vertical ascendente sometidos a la acción desaceleradora de la gravedad, como un disparo vertical; o a cualquier objeto (satélites naturales o artificiales, planetas, etc.) en órbita alrededor de un cuerpo celeste. Otros sucesos referidos también como caída libre lo constituyen las trayectorias geodésicas en el espacio-tiempo descritas en la teoría de la relatividad general.
Ejemplos de caída libre deportiva los encontramos en actividades basadas en dejarse caer una persona a través de la atmósfera sin sustentación alar ni de paracaídas durante un cierto trayecto.
TIRO VERTICAL
El tiro vertical, cuya dirección puede ser descendente o ascendente, tiene una velocidad inicial que resulta diferente a cero. El cuerpo en cuestión se lanza hacia arriba, impulsado con una cierta velocidad. Luego regresa al punto de partida con la misma velocidad, aunque en un sentido contrario a la que tenía en el momento del lanzamiento.Puede decirse, de este modo, que el cuerpo lanzado en un tiro vertical sube y luego baja, regresando al punto de partida. Cuando el cuerpo alcanzó la altura máxima, la velocidad resulta nula. En ese instante, el cuerpo deja de subir e inicia su descenso. El tiempo que el cuerpo demora en llegar a la altura máxima resulta idéntico al tiempo que tarda en volver a su punto de partida.
Un ejemplo de tiro vertical se produce cuando tomamos una pelota de tenis con una mano y la lanzamos hacia arriba en línea recta. Dicha pelota subirá durante una breve fracción de tiempo, llegará a su altura máxima y luego descenderá, volviendo a nuestra mano. En la práctica, de todos modos, el tiro vertical puede resultar complicado de realizar ya que el lanzamiento puede no ser recto, el viento puede influir en la pelota, etc.
PROBLEMAS DE CAÍDA LIBRE
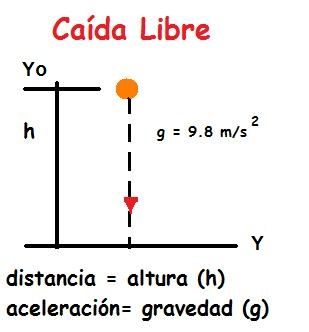
Ejercicio 1. Un cuerpo cae libremente desde el reposo durante 6 segundos hasta llegar al suelo. Calcular la distancia que ha recorrido, o lo que es lo mismo, la altura desde donde se soltó.
Datos que tenemos:
Velocidad inicial ………. Vo = 0 (la soltamos y parte de velocidad cero)
Tiempo de caída …….…... t = 6 s
Aceleración de caída …... g = 10 m/s2 (aproximamos en lugar de 9,8)
Altura final será el suelo = 0 (Nota: aunque no fuera el suelo en caída libre la altura final siempre = 0)
Parte de una altura inicial Yo = ??? es la que nos piden, también podemos llamarla altura o "h".
Aplicaremos la segunda fórmula :
Y = vo t + Yo - 0.5 gt² donde Yo será la altura inicial o altura desde la que cae (h).
poniendo valores en la fórmula :
0 = Yo -0.5 ( 10 x 6²) ==> despejando Yo
-Yo = - 180 Los signos menos se nos marchan en los dos miembros de la ecuación y quedarán positivos.
Yo = 180m Resuelto h = 180 metros
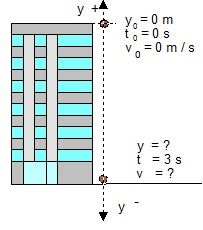
Ejercicio 2. Un tornillo cae accidentalmente desde la parte superior de un edificio. 4 segundos después está golpeando el suelo. ¿Cual será la altura del edificio?.
Datos iniciales:
Velocidad inicial ................... Vo = 0
tiempo de caída ...................... t = 4s
aceleración de caída ............... g = 10 m/s2
altura de caída (edificio ) .......... h = ? (en la fórmula será Yo)
Aplicamos la segundo fórmula Y = vo t + Yo - 0.5 gt² o lo que es lo mismo Y = Vo . t - 1/2 gt². En nuestro caso tenemos qué:
0 = Yo - 1/2 ( 10 x 4²) = => 0 = Yo - 80 ;despejando Yo
Yo = 80 metros Resuelto
Ejercicio 3. Desde el techo de un edificio se deja caer una piedra hacia abajo y se oye el ruido del impacto contra el suelo 3 segundos después. Sin tomar en cuenta la resistencia del aire, ni el tiempo que tardó el sonido en llegar al oído, calcula:
a) La altura del edificio.
b) La velocidad de la piedra al llegar al suelo.
Considerar g = 10 m/s²
Primero calculamos el apartado b). Aplicamos la primera fórmula: V = Vo +- gt, para calcular la velocidad a la que llega al suelo, sabiendo que Vo = cero y que el signo es + por ir cada vez más rápido la piedra. La fórmula quedará V = gt
V = 10 x 3 = 30 m/s Resuelto.
Ahora para el apartado a) aplicamos la segundo fórmula sabiendo que Y (final) es cero por que acaba en el suelo y la Vo sigue siendo cero también. La fórmula quedará:
Y = Yo - 0.5 gt²
0 = Yo - (0.5 x 10 x 3²) = Yo - 35 Despejando Yo tenemos:
Yo = 45 metros Resuelto.
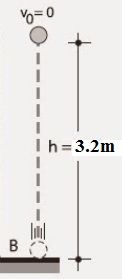
Ejercicio 4. ¿Con qué velocidad se debe lanzar hacia arriba, una piedra, para que logre una altura máxima de 3.2 m?
Datos iniciales:
Velocidad inicial ............. Vo = ?
Velocidad final ................ Vf = 0 (cuando llega a la altura máxima y se para)
altura máxima alcanzada .. Y = 3,2 m
altura inicial Yo = 0 (se lanza desde el suelo)
aceleración actuante ........ g = 10 m/s2
Aplicaremos la tercera fórmula ya que no nos dan el tiempo:
Vf² = Vo² - 2g( Y – Yo)
0 = Vo² - 2 x 10 ( 3,2 - 0) =
0 = Vo² - 64 despejamos la velocidad inicial del lanzamiento Vo ===>
Vo = √ 64 m/s = 8m/s Resuelto
Ejercicio 5. Hallar la velocidad con que fue lanzado un proyectil hacia arriba si ésta se reduce a la tercera parte cuando ha subido 40 m. (g = 10 m/s2)
Datos iniciales
La velocidad inicial es 3 veces mayor que la inicial, ya que se redujo 3 veces. La Yo se considera el suelo luego Yo = 0
Velocidad final .............. Vf = Vo/3 de aquí despejamos Vo y tenemos ==>
Velocidad inicial..............Vo = Vf x 3
altura ............................. h = 40m
aceleración de subida ...... g = -- 10 m/s2
Aplicamos la tercera fórmula V² - Vo² = - 2g( Y – Yo) y donde pone Vo ponemos = V x 3 ( 3 veces mayor como nos dice el problema)
V² - Vo² = - 2g( Y – Yo) ==> V² - (3V)² = - 2 x 10( 40 – 0) quedará:
V² - 9V² = - 800
OJO (3V)² son 3V² x 3V² = 9V² (OJO NO puedes hacer V² - 3Vo² = 2 V² estaría mal)
-8V² = -800 ==> Podemos cambiar los signos menos por más ya que están a los dos lados de la ecuación.
V² = 800/8 = 100 Luego...
V = √100 = 10 m/s Resuelto
Datos que tenemos:
Velocidad inicial ………. Vo = 0 (la soltamos y parte de velocidad cero)
Tiempo de caída …….…... t = 6 s
Aceleración de caída …... g = 10 m/s2 (aproximamos en lugar de 9,8)
Altura final será el suelo = 0 (Nota: aunque no fuera el suelo en caída libre la altura final siempre = 0)
Parte de una altura inicial Yo = ??? es la que nos piden, también podemos llamarla altura o "h".

Aplicaremos la segunda fórmula :
Y = vo t + Yo - 0.5 gt² donde Yo será la altura inicial o altura desde la que cae (h).
poniendo valores en la fórmula :
0 = Yo -0.5 ( 10 x 6²) ==> despejando Yo
-Yo = - 180 Los signos menos se nos marchan en los dos miembros de la ecuación y quedarán positivos.
Yo = 180m Resuelto h = 180 metros
Ejercicio 2. Un tornillo cae accidentalmente desde la parte superior de un edificio. 4 segundos después está golpeando el suelo. ¿Cual será la altura del edificio?.
Datos iniciales:
Velocidad inicial ................... Vo = 0
tiempo de caída ...................... t = 4s
aceleración de caída ............... g = 10 m/s2
altura de caída (edificio ) .......... h = ? (en la fórmula será Yo)
Aplicamos la segundo fórmula Y = vo t + Yo - 0.5 gt² o lo que es lo mismo Y = Vo . t - 1/2 gt². En nuestro caso tenemos qué:
0 = Yo - 1/2 ( 10 x 4²) = => 0 = Yo - 80 ;despejando Yo
Yo = 80 metros Resuelto
Ejercicio 3. Desde el techo de un edificio se deja caer una piedra hacia abajo y se oye el ruido del impacto contra el suelo 3 segundos después. Sin tomar en cuenta la resistencia del aire, ni el tiempo que tardó el sonido en llegar al oído, calcula:
a) La altura del edificio.
b) La velocidad de la piedra al llegar al suelo.
Considerar g = 10 m/s²

Primero calculamos el apartado b). Aplicamos la primera fórmula: V = Vo +- gt, para calcular la velocidad a la que llega al suelo, sabiendo que Vo = cero y que el signo es + por ir cada vez más rápido la piedra. La fórmula quedará V = gt
V = 10 x 3 = 30 m/s Resuelto.
Ahora para el apartado a) aplicamos la segundo fórmula sabiendo que Y (final) es cero por que acaba en el suelo y la Vo sigue siendo cero también. La fórmula quedará:
Y = Yo - 0.5 gt²
0 = Yo - (0.5 x 10 x 3²) = Yo - 35 Despejando Yo tenemos:
Yo = 45 metros Resuelto.
Ejercicio 4. ¿Con qué velocidad se debe lanzar hacia arriba, una piedra, para que logre una altura máxima de 3.2 m?
Datos iniciales:
Velocidad inicial ............. Vo = ?
Velocidad final ................ Vf = 0 (cuando llega a la altura máxima y se para)
altura máxima alcanzada .. Y = 3,2 m
altura inicial Yo = 0 (se lanza desde el suelo)
aceleración actuante ........ g = 10 m/s2

Aplicaremos la tercera fórmula ya que no nos dan el tiempo:
Vf² = Vo² - 2g( Y – Yo)
0 = Vo² - 2 x 10 ( 3,2 - 0) =
0 = Vo² - 64 despejamos la velocidad inicial del lanzamiento Vo ===>
Vo = √ 64 m/s = 8m/s Resuelto
Ejercicio 5. Hallar la velocidad con que fue lanzado un proyectil hacia arriba si ésta se reduce a la tercera parte cuando ha subido 40 m. (g = 10 m/s2)
Datos iniciales
La velocidad inicial es 3 veces mayor que la inicial, ya que se redujo 3 veces. La Yo se considera el suelo luego Yo = 0
Velocidad final .............. Vf = Vo/3 de aquí despejamos Vo y tenemos ==>
Velocidad inicial..............Vo = Vf x 3
altura ............................. h = 40m
aceleración de subida ...... g = -- 10 m/s2
Aplicamos la tercera fórmula V² - Vo² = - 2g( Y – Yo) y donde pone Vo ponemos = V x 3 ( 3 veces mayor como nos dice el problema)
V² - Vo² = - 2g( Y – Yo) ==> V² - (3V)² = - 2 x 10( 40 – 0) quedará:
V² - 9V² = - 800
OJO (3V)² son 3V² x 3V² = 9V² (OJO NO puedes hacer V² - 3Vo² = 2 V² estaría mal)
-8V² = -800 ==> Podemos cambiar los signos menos por más ya que están a los dos lados de la ecuación.
V² = 800/8 = 100 Luego...
V = √100 = 10 m/s Resuelto
No hay comentarios:
Publicar un comentario