MRUA
El movimiento rectilíneo uniformemente acelerado (MRUA), también conocido como movimiento rectilíneo uniformemente variado (MRUV), es aquel en el que un móvil se desplaza sobre una trayectoria recta estando sometido a una aceleración constante.
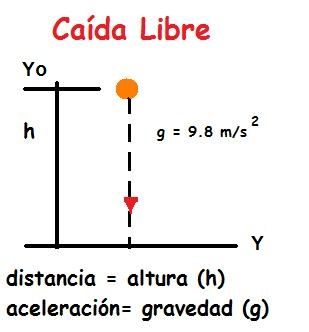
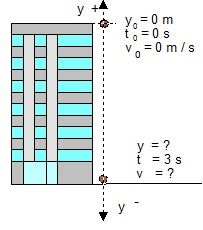
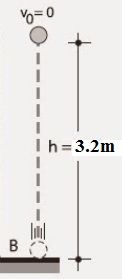
Un ejemplo de este tipo de movimiento es el de caída libre vertical, en el cual la aceleración interviniente, y considerada constante, es la que corresponde a la gravedad.
También puede definirse como el movimiento que realiza una partícula que partiendo del reposo es acelerada por una fuerza constante.
El movimiento rectilíneo uniformemente acelerado (MRUA) es un caso particular del movimiento uniformemente acelerado (MUA).
Concepto de aceleración
La aceleración es la consecuencia del
verbo acelerar, vocablo de origen latino, proveniente de “celer” que significa
ir más rápido.
En Física se conoce como aceleración el cambio que sufre la velocidad de
un cuerpo en determinado tiempo. Se necesita saber su dirección, magnitud y
sentido, por tratarse de una magnitud vectorial que establece una relación entre
las variaciones de velocidad y el tiempo en que tardan en producirse.. En el
sistema internacional la unidad es el m/s2. Se
mide con un acelerómetro. Lo que indica la aceleración es cuán rápido suceden
los cambios de velocidad y no la velocidad en sí misma. Un objeto puede moverse
con mucha rapidez y no ser mucha su aceleración. Si la velocidad es constante,
la aceleración es igual a cero, por más que se mueva rápidamente. La
aceleración negativa se denomina desaceleración. Esto sucede por ejemplo cuando
un vehículo frena.
El movimiento es uniformemente acelerado si el aumento es
proporcional al tiempo.
DESACELERACIÓN
Es la variación negativa de la velocidad, o sea la magnitud física que expresa el paso de un cuerpo en movimiento de una velocidad a otra velocidad inferior, siguiendo siempre la misma trayectoria. Dicho término puede definirse también como aceleración negativa.
Un ejemplo típico de deceleración es el que ofrece un vehículo en fase de frenado. Varios son los fenómenos que se verifican en el espacio de tiempo comprendido entre el inicio de la deceleración y la parada del vehículo. Uno de los más evidentes es el de la mayor carga que actúa sobre el puente delantero y el consiguiente aligeramiento del puente trasero.
En efecto, durante el frenado además del peso interviene la fuerza de inercia que, aplicada sobre el baricentro del coche, actúa longitudinalmente en la misma dirección que el movimiento. Dicha fuerza da lugar a un momento de vuelco longitudinal que aumenta la porción de peso del vehículo sobre las ruedas delanteras y reduce la de las traseras. Se produce, pues, lo que se define como una transferencia de carga del eje trasero al delantero.
El desplazamiento de peso determina a su vez una variación de adherencia entre las ruedas delanteras (más cargadas y por tanto más adherentes) y las traseras (menos cargadas y menos adherentes). La tendencia de las ruedas a patinar se aprecia mucho más en las traseras que en las delanteras. Por esto, muchos coches disponen de un limitador de frenado, es decir, de un dispositivo que disminuye la fuerza frenante en las ruedas traseras, reduciendo con ello el peligro de bloqueo y, por consiguiente, de deslizamiento.
Problema 1
Supongamos que un automóvil. parte del reposo y se acelera hasta una velocidad de 10 m/s en una trayectoria rectilínea en 5 Seg, como muestra la línea recta de la figura 1. Encontremos suaceleración media.
Figura 1
Análisis gráfico
Al observar la línea diagonal de la figura 1, notamos la variación de la velocidad y del tiempo de un automóvil que experimenta unaaceleración uniforme de 2m/s cada segundo. Esto lo podemos notar en la gráfica, ya que, el tiempo (línea horizontal) y la velocidad (línea vertical) en las parejas ordenas (0 , 0); (1 , 2); (2 , 4); (3 , 6); van variando de uno en uno el tiempo y la velocidad de dos en dos.
Análisis matemático
De la grafica podemos observar que:
Vi = 0 m/s
t = 5s
Vf =10 m/s
sustituyendo en la ecuación de la aceleración media, tenemos:
Lo cual lo leemos: 2 metros por Segundo cada Segundo, o 2 metros por segundo por segundo.
En otras palabras, la velocidad del automóvil se incrementen 2m/s cada segundo, y esta relación de incremento de la velocidad es la cantidad a la que se llama aceleración. El resultado anterior para ase escribe con frecuencia como 2 m/s2 y se lee 2 metros porsegundos al cuadrado.
En general, la unidad de a será una unidad de distancia dividida entre el producto de dos unidades de tiempo. Las unidades podrían ser; millas por segundos cuadrados, pies por segundo por hora, centímetros por segundos por minutos, millas por hora por segundo, y así sucesivamente.
Problema 2
Un automóvil parte del reposo y acelera uniformemente hasta alcanzar una rapidez de 20 m/s en 4 segundos. Determinar siaceleración y la distancia recorrida.
Problema 3
Un indígena dispara una fecha, la cual sale diparada en línea recta durante 0.5 segundos después de estar en posición de martillado, si ésa alcanza una velocidad de 40 m/s en éste tiempo, ¿cuál fue la aceleración?
Solución
Los datos e incógnita que tenemos del problema son:
En el problema podemos detallar que la posición inicial de la Flecha es de martillado, por lo que se asumimos que está en reposo, es decir, que la Velocidad Inicial es de “0”, además le asignamos las unidades m/s, porque la cantidad númerica es cero y la velocidad final esta en m/s.
t = 0.5 seg
Vi = 0 m/s
Vf = 40 m/s
a = ?
Al sustituir los valores numéricos en la ecuación de aceleración, obtenemos:
La aceleración de la flecha es de 80 m/s2